Mentor: Jeffrey L. Kauffman
Description: Increasing use of composite materials for hot components enables lighter aerostructures with unique anisotropic coupling not possible with traditional materials. However, anisotropy makes predicting vibratory and flutter response extremely difficult, especially when operated in a wide range of temperature and membrane loads. Applied loads create complex stress and strain distributions in the laminate; moreover, different coefficients of thermal expansion (CTEs) generate further intra-laminar stresses under thermal loading. Recent research using a modal strain energy method demonstrated how in-plane loads affect damping of isotropic beams and plates with distributions that are uniform through the thickness. Additional research has created new viscous damping models with terms that directly relate to well-understood energy-dissipation mechanisms in these structures. It is hypothesized that modifying a modal strain energy approach will make possible component-level computations of equivalent damping parameters. Using CTEs and composite geometry enables computation of the thermally-induced strain. Finally, weighting each component’s dissipation by its energy fraction will yield a component-level damping that depends on composite geometry and thermal and mechanical loads.
After training, the REU students working on this task will conduct dynamic tests, derive analytical models and simulate dynamic behavior. Students will learn to fabricate test articles and design test fixtures that generate desired multi-axial loading with prescribed boundary conditions, calculate strain distributions and effective strain energy densities in composite laminates, and create computational algorithms that predict the effects of thermal and membrane loads on a structure’s vibratory response. These tasks will prepare students for future experimental, theoretical and computational research in graduate school. Students will present research posters and contribute as co-author to journal publications.
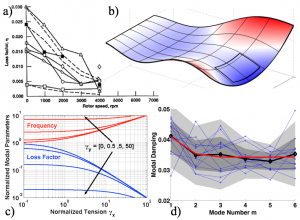
Tensile loads reduce damping (a); modal strain energy (b) enables damping prediction (c); novel viscous damping models match test data (d).